
正弦電流電路中的有功功率、無功功率、和視在功率三者之間是一個直角三角形的關系,可以通過“復功率”來表示。若用視在功率S表示復功率,則有功功率P為復功率的實部,而無功功率Q為復功率的虛部。在非正弦電路中,無功功率的定義發生了改變,為了與正弦電路的定義相統一,補充了位移無功功率和畸變無功功率的概念,兩者的方和根稱為廣義無功功率。
在具有電感和電容等儲能元件的電路中,儲能元件在半周期的時間里把電源能量變成磁場(或電場)的能量儲存起來,在另半周期的時間里對已存的磁場(或電場)能量返回給電源,由于這部分能量只是在儲能元件與電源之間進行能量交換,并沒有真正被消耗,我們把單位時間內交換能量的振幅值稱為無功功率。
無功功率用符號Q表示。
在《GB/T 2900.1-2008 電工術語 基本術語》中,對無功功率(reactive power)定義如下:
對于正弦狀態下線性二端元件或二端電路,其量值等于視在功率S和(端子間電壓對電流的)相位移角φ的正弦之乘積的量。
在國際單位制(SI)中,無功功率的單位為伏安(VA)。在IEC60027-1中給出了無功功率的專用單位名稱“乏”和符號Var。
無功功率的常用單位還有毫乏(mvar)、千乏(kvar)、兆乏(Mvar)等。
假設交流電周期為T,電壓、電流的瞬時值表達式分別為u(t)、i(t),正弦電路中,電壓、電流及瞬時功率的表達式為:
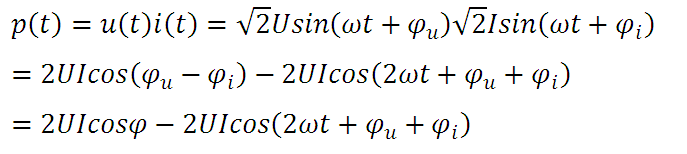
正弦穩態電路的瞬時功率表達式
式中:U、I為電壓、電流的有效值,ω為角速度,φu為電壓的初始相位,φu為電流的初始相位,φ為電壓與電流的相位差,即:電流滯后于電壓的相位移。
因此,正弦穩態電路中,如下圖,只要φ≠0°,瞬時功率就會出現負數,表明該電路既會消耗功率,也能發出功率。
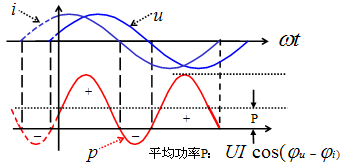
正弦穩態電路中的瞬時功率波形圖
式中前半部分為常數;后半部分在-2UI和2UI之間變化,且在一個周期內的平均值為零。
瞬時功率p(t)在一個周期內的平均值為2UIcosφ。我們稱P=2UIcosφ為有功功率。
正弦穩態中,儲能元件電感或電容的平均功率等于零,不消耗能量,但和電源之間存在能量的交換作用,即在前半個周期吸收電源的功率并儲存起來,后半個周期又將其全部釋放,這種能量交換的幅度用另外一種功率——無功功率來描述。
若將電壓相量與電流相量的共軛復數的乘積用復功率表示,其表達式為:
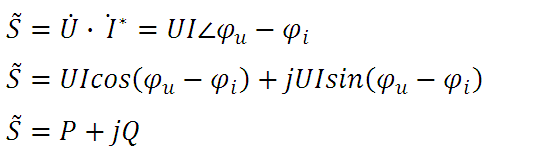
有功功率、無功功率、視在功率及復功率
復功率的實部為有功功率,虛部為無功功率,復功率的模為視在功率,這樣,有功功率、無功功率、和視在功率三者之間是一個直角三角形的關系。
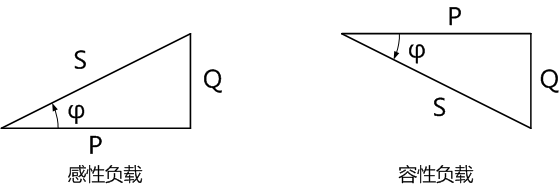
有功功率和無功功率及視在功率構成的復功率三角形
在非正弦電路中,有功功率和視在功率的定義不變,然而,此時,電壓、電流相位差已經沒有明確的物理意義,此時,Q按照下述公式定義:
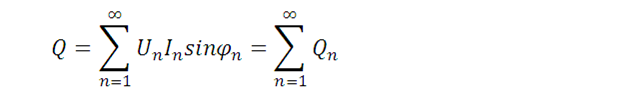
式中,Un、In為n次諧波的有效值,當n=1時,U1、I1稱為基波有效值。
然而,此時,
![]()
為此,引入畸變無功功率D,使下式成立:
![]()
Q是相同頻率的電壓分量與電流分量相位移不同產生的無功,稱為位移無功功率。而畸變無功功率則是不同頻率電壓及電流分量之間產生的無功,畸變無功功率計算式如下:
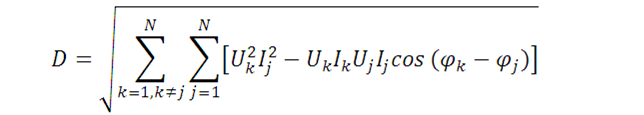
某些文獻中也將Q稱為無功功率,而將Q和D的方和根稱為廣義無功功率。
如下圖所示,依據電壓與電流的相位差,在0~360°四個象限內,無功功率和無功功率的正負號不同,含義也不同。
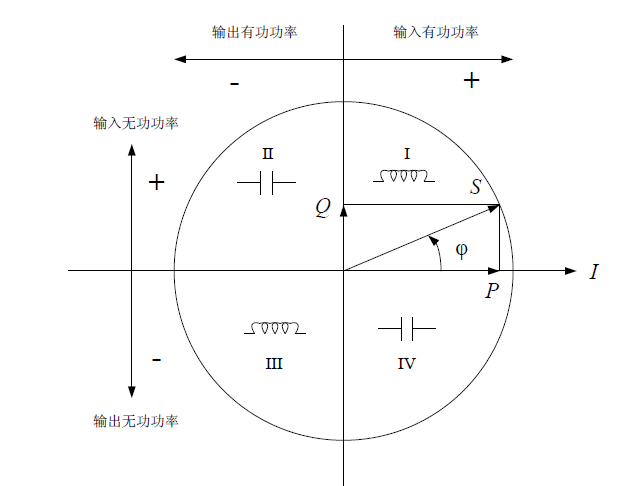
四象限無功功率示意圖
第一象限為感性負載,輸入無功功率為正,輸入有功功率為正,可用L+表示;
第二象限為容性電源,輸入無功功率為正,輸入有功功率為負,可用C+表示;
第三象限為感性電源,輸入無功功率為負,輸入有功功率為負,可用L-表示;
第四象限為容性負載,輸入無功功率為負,輸入有功功率為正,可用C-表示。
按照變頻電量的定義,非正弦電量屬于變頻電量,全面、準確的測量變頻電量的各種特征值,應采用變頻功率傳感器(或獨立的電壓、電流傳感器)及變頻功率分析儀。
由于無功功率的定義存在一定的分歧,AnyWay的WP4000變頻功率分析儀等儀器在測量非正弦電量時,儀表本身只顯示有功功率,無功功率可則通過上位機擴展軟件計算顯示,用戶可根據不同的定義式選擇需要的無功功率。

可測量位移無功功率、畸變無功功率的WP4000變頻功率分析儀
擴展閱讀: