一、定義

　　基波有效值（Fundamental wave effective value）是指交流信號的基波分量的方均根值。

二、周期信號分析

　　一個周期信號可以通過傅里葉變換分解為直流分量c0和不同頻率的正弦信號的線性疊加：

　　

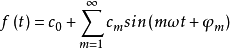
　　其中，c_m表示m次諧波的幅值，其角頻率為mω，初始相位為φ_m，其有效值為c_m/√2。

　　當m=1時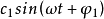，為基波分量的表達式，其角頻率為ω，初始相位為φ1，其方均根值c1/√2稱為基波有效值。ω/2π為基波分量的頻率，稱為基波頻率，基波分量的頻率等于交流信號的頻率。而m次諧波的頻率為基波頻率的整數倍（m倍）。

三、修正平均值與基波有效值的區別

　　修正值平均值也稱校準到有效值的整流平均值，簡稱校準平均值（mean）。顧名思義，就是將整流平均值乘以一個系數，使其結果等于該信號的有效值。這個系數是π/（2√2）≈1.1107。

　　由于其修正系數的基于正弦波獲取的，所以，適合正弦波信號。換言之，該方法不能適用于所有信號。

　　除了正弦波外，mean值在數值上還接近正弦調制PWM的基波有效值。也正因為這個原因，有人提出可以用mean值取代變頻器電壓波形的基波有效值。需要注意的是：

　　首先，“取代”僅指電壓信號。電流信號則無此規律。比如，PWM信號經過某非線性的、感性的負載，電流信號包含了較大的低次諧波，而高次諧波含量非常小，此時，mean值與基波有效值差距較大。

其次，校準平均值應用與變頻器的PWM測試，若精度要求高，有若干前提：

　　1、正弦調制

　　2、開關頻率足夠高

　　3、開關頻率是基波頻率的整倍數等等

　　顯然，許多情況下，上述條件并不能完全滿足。尤其是第一條，如今，變頻調速技術發展迅速，非正弦調制的變頻器越來越多，對于一般用戶，可能根本不知道其變頻器采用何種調制方式，此時，貿然的采用mean值去替代基波有效值測試，可能會帶來較大的誤差。尤其是應用于電機試驗，很可能造成對電機質量的誤判及對設計驗證的誤導。

　　因此，國家標準的要求是正確的。時過境遷，任何技術都有其時代背景，都有其局限性。可以說，在變頻測試中，mean值可以取代變頻器基波有效值測試的觀點，已經逐漸過時了。

四、測量方法

　　當信號的諧波頻率與基波頻率差距較大時，即信號的低次諧波含量較小，主要為高次諧波時，可以通過低通濾波的方法將高次諧波濾除，剩下就是信號的基波，采用均值檢波表、峰值檢波表和真有效值檢波表均可測量其有效值，測量結果近似等于基波有效值。

　　當信號頻譜較復雜時，尤其是低次諧波含量較大時，很難用濾波的方法將基波準確分離，一般先用交流采樣獲取離散時間信號序列，再用離散傅里葉變換（DFT或FFT）對其進行傅里葉展開，即可求得基波有效值。各種諧波分析儀和寬頻功率分析儀（變頻功率分析儀、高精度功率分析儀等）等設備均可測量適用頻率范圍內交流信號的基波有效值。上述儀器除了測量電壓、電流的基波有效值之外，還具備功率測量及諧波測量功能。

可以測量基波有效值的WP4000變頻功率分析儀

---