
在電工技術中,將單口網絡端鈕電壓和電流有效值的乘積,稱為視在功率(apparent power),記為S=UI。只有單口網絡完全由電阻混聯而成時,視在功率才等于平均功率,否則,視在功率總是大于平均功率(即有功功率),也就是說,視在功率不是單口網絡實際所消耗的功率。為以示區別,視在功率不用瓦特(W)為單位,而用伏安(VA)或千伏安(kVA)為單位。
《GB/T2900.1-2008 電工術語 基本術語》對視在功率定義如下:
二端元件或二端電路端子間電壓的方均根值U與該元件或電路中的電流的方均根值I的乘積。
由于視在功率等于網絡端鈕處電流、電壓有效值的乘積,而有效值能客觀地反映正弦量的大小和他的做功能力,因此這兩個量的乘積反映了為確保網絡能正常工作,外電路需傳給網絡的能量或該網絡的容量。
由于網絡中既存在電阻這樣的耗能元件,又存在電感、電容這樣的儲能元件,所以,外電路必須提供其正常工作所需的功率,即平均功率或有功功率,同時應有一部分能量被貯存在電感、電容等元件中。這就是視在功率大于平均功率的原因。只有這樣網絡或設備才能正常工作。若按平均功率給網絡提供電能是不能保證其正常工作的。
因此,在實際中,通常是用額定電壓和額定電流來設計和使用用電設備的,用視在功率來標示它的容量。
另外,由于電感、電容等元件在一段時間之內儲存的能量將分別在其它時間段內釋放掉,這部分能量可能會被電阻所吸收,也可能會提供給外電路。所以,我們看到單口網絡的瞬時功率有時為正有時為負。
在正弦穩態電路中,整個RLC串聯電路中吸收的瞬時功率為:
p=pR+pC+pL=RI2[1+cos(2ωt)]-(ωL-1/ωC)I2sin(2ωt)
它是一個頻率為正弦電流或電壓頻率2倍的周期量。第一項始終是大于或等于零,是瞬時功率的不可逆部分,為電路所吸收的功率,不再返回外部電路。
第二項表明,電感和電容的瞬時功率反相,在能量交換過程中,彼此互補,電感吸收或釋放能量時,恰好是電容釋放或吸收能量。彼此互補后的不足部分由外部電路補充。
在正弦穩態電路中,有功功率一般小于視在功率,也就是說視在功率上打一個折扣才能等于平均功率,這個折扣稱為功率因數(power factor),數值上等于位移因數(電壓與電流的相位差的余弦值,用cosφ表示)。
正弦交流電路中,下述等式成立:
P=S*cosφ
Q=S*sinφ
P2+Q2=S2
可見,視在功率S與有功功率P和無功功率Q在數值上呈現一個三角形關系。
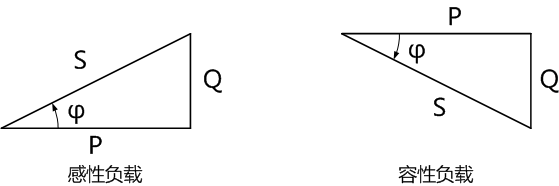
視在功率與有功功率和無功功率構成的復功率三角形
在非正弦電路中,無功功率、有功功率的定義式有所不同,等式P2+Q2=S2也不再成立,詳細內容請參見銀河百科詞條“廣義無功功率”。
值得注意的是,視在功率的標準定義只針對二端電路。在三相不平衡正弦電路中,三相視在功率與作為二端電路的每一相電路的視在功率之間應該如何換算呢?是簡單的數值相加,還是有其它的計算方法呢?詳情請參見“如何計算三相不平衡正弦電路的視在功率和功率因數?”。
銀河百科:有功功率