
一小波定義
小波(Wavelet)這一術語,顧名思義,“小波”就是小區域、長度有限、均值為0的波形。所謂“小”是指它具有衰減性;而稱之為“波”則是指它的波動性,其振幅正負相間的震蕩形式。與Fourier變換相比,小波變換是時間(空間)頻率的局部化分析,它通過伸縮平移運算對信號(函數)逐步進行多尺度細化,最終達到高頻處時間細分,低頻處頻率細分,能自動適應時頻信號分析的要求,從而可聚焦到信號的任意細節,解決了Fourier變換的困難問題,成為繼Fourier變換以來在科學方法上的重大突破。有人把小波變換稱為“數學顯微鏡”。被廣泛應用于調和分析、語音處理、圖像分割、石油勘探和雷達探測等等方面,也被應用于音頻、圖像和視頻的壓縮編碼。
二小波分析
與Fourier變換相比,小波變換是空間(時間)和頻率的局部變換,因而能有效地從信號中提取信息。通過伸縮和平移等運算功能可對函數或信號進行多尺度的細化分析,解決了Fourier變換不能解決的許多困難問題。小波變換聯系了應用數學、物理學、計算機科學、信號與信息處理、圖像處理、地震勘探等多個學科。數學家認為,小波分析是一個新的數學分支,它是泛函分析、Fourier分析、樣調分析、數值分析的完美結晶;信號和信息處理專家認為,小波分析是時間—尺度分析和多分辨分析的一種新技術,它在信號分析、語音合成、圖像識別、計算機視覺、數據壓縮、地震勘探、大氣與海洋波分析等方面的研究都取得了有科學意義和應用價值的成果。 信號分析的主要目的是尋找一種簡單有效的信號變換方法,使信號所包含的重要信息能顯現出來。小波分析屬于信號時頻分析的一種,在小波分析出現之前,傅立葉變換是信號處理領域應用最廣泛、效果最好的一種分析手段。傅立葉變換是時域到頻域互相轉化的工具,從物理意義上講,傅立葉變換的實質是把這個波形分解成不同頻率的正弦波的疊加和。正是傅立葉變換的這種重要的物理意義,決定了傅立葉變換在信號分析和信號處理中的獨特地位。傅立葉變換用在兩個方向上都無限伸展的正弦曲線波作為正交基函數,把周期函數展成傅立葉級數,把非周期函數展成傅立葉積分,利用傅立葉變換對函數作頻譜分析,反映了整個信號的時間頻譜特性,較好地揭示了平穩信號的特征。
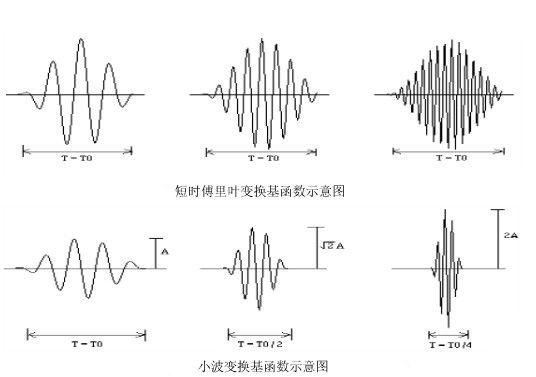
小波變換是一種新的變換分析方法,它繼承和發展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點,能夠提供一個隨頻率改變的時間一頻率窗口,是進行信號時頻分析和處理的理想工具。它的主要特點是通過變換能夠充分突出問題某些方面的特征,因此,小波變換在許多領域都得到了成功的應用,特別是小波變換的離散數字算法已被廣泛用于許多問題的變換研究中。從此,小波變換越來越引起人們的重視,其應用領域來越來越廣泛。
現在,它已經在科技信息產業領域取得了令人矚目的成就。電子信息技術是六大高新技術中重要的一個領域,它的重要方面是圖象和信號處理。現今,信號處理已經成為當代科學技術工作的重要部分,信號處理的目的就是:準確的分析、診斷、編碼壓縮和量化、快速傳遞或存儲、精確地重構(或恢復)。從數學地角度來看,信號與圖象處理可以統一看作是信號處理(圖象可以看作是二維信號),小波分析的許多分析和應用問題,都可以歸結為信號處理問題。現在,對于其性質隨時間是穩定不變的信號(平穩隨機過程),處理的理想工具仍然是傅立葉分析。但是在實際應用中的絕大多數信號是非穩定的(非平穩隨機過程),而特別適用于非穩定信號的工具就是小波分析。
三小波變換應用
小波分析的應用領域十分廣泛,它包括:數學領域的許多學科;信號分析、圖象處理;量子力學、理論物理;軍事電子對抗與武器的智能化;計算機分類與識別;音樂與語言的人工合成;醫學成像與診斷;地震勘探數據處理;大型機械的故障診斷等方面;例如,在數學方面,它已用于數值分析、構造快速數值方法、曲線曲面構造、微分方程求解、控制論等。在信號分析方面的濾波、去噪聲、壓縮、傳遞等。在圖象處理方面的圖象壓縮、分類、識別與診斷,去污等。在醫學成像方面的減少B超、CT、核磁共振成像的時間,提高分辨率等。
1、小波分析用于信號與圖象壓縮是小波分析應用的一個重要方面。它的特點是壓縮比高,壓縮速度快,壓縮后能保持信號與圖象的特征不變,且在傳遞中可以抗干擾。基于小波分析的壓縮方法很多,比較成功的有小波包最好基方法,小波域紋理模型方法,小波變換零樹壓縮,小波變換向量壓縮等;
2、小波分解可以覆蓋整個頻域(提供了一個數學上完備的描述;
3、小波變換具有“變焦”特性,在低頻段可用高頻率分辨率和低時間分辨率(寬分析窗口),在高頻段,可用低頻率分辨率和高時間分辨率(窄分析窗口);
4、小波變換實現上有快速算法(Mallat小波分解算法);
從圖像處理的角度看,小波變換存在以下幾個優點:
1、小波分解可以覆蓋整個頻域(提供了一個數學上完備的描述)
2、小波變換通過選取合適的濾波器,可以極大的減小或去除所提取得不同特征之間的相關性
3、小波變換具有“變焦”特性,在低頻段可用高頻率分辨率和低時間分辨率(寬分析窗口),在高頻段,可用低頻率分辨率和高時間分辨率(窄分析窗口)
4、小波變換實現上有快速算法(Mallat小波分解算法)